Solved it several ways. It's cool, but what relevance does this have to chess?
Chess and Mathematics - 2
Sort:
Mar 20, 2017
0
#3
@remlu could you please share your solutions with us? The main objective is of course mathematics, chess is a tool here.
Mar 20, 2017
0
#4
remlu wrote:
Why does everything only have to be about strictly how to use it for chess, mathematics is also very beautiful and chess offers fun rules and constraints to toy with ideas for fun
Solved it several ways. It's cool, but what relevance does this have to chess?
Mar 20, 2017
0
#5
ynaliyev wrote:
Well there is at least four answers right? if you mirror the knight on each of the corners in the same position it would be the same geometry. Or is that cheating :)
Four Knights Problem
Legend about the four diamonds
Divide the board into four regions of equal shape so that each knight belongs to one of the regions. One of the possible answers is the following:
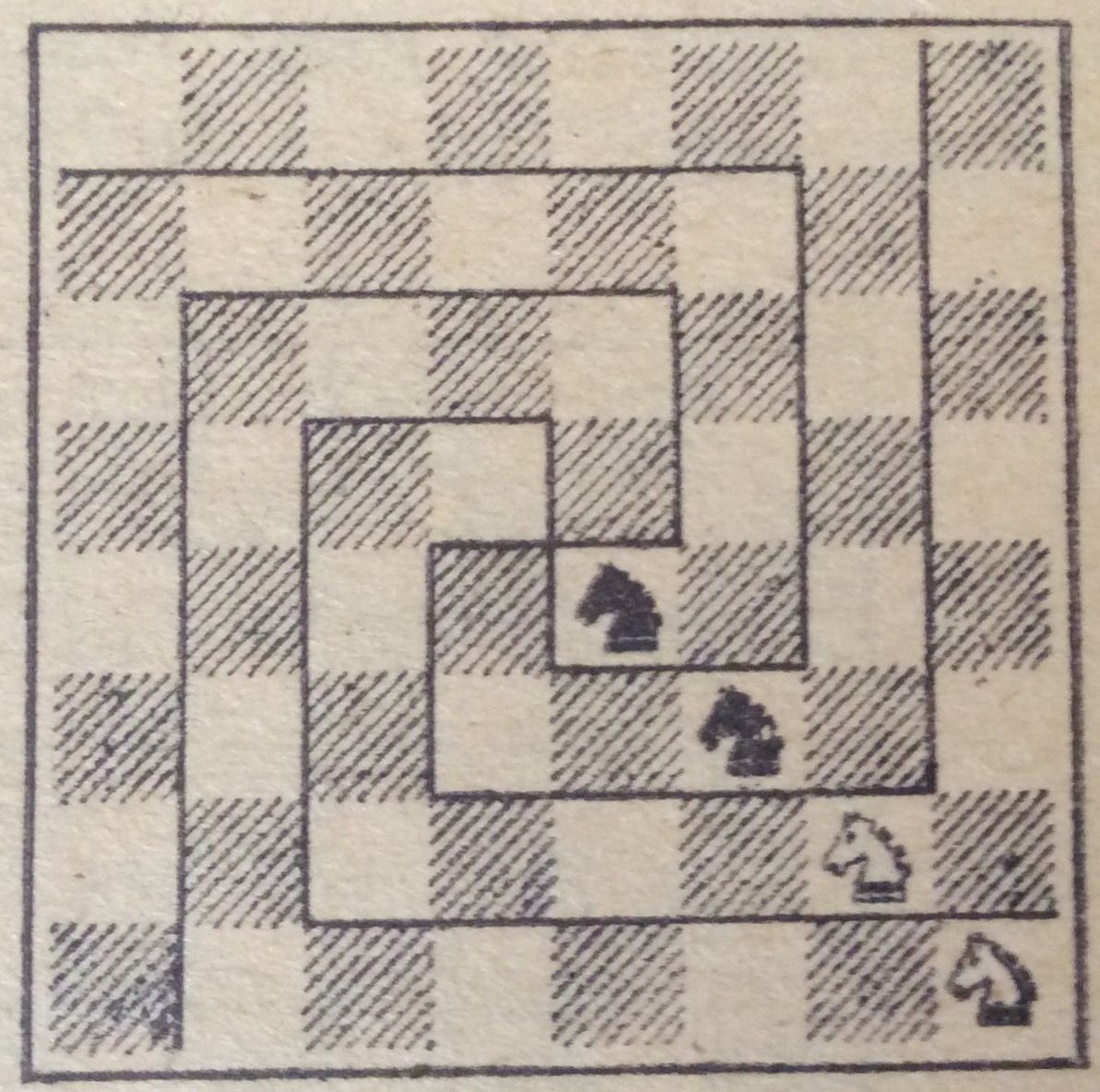
Can you find the other solutions of this problem? Write in the comments. If the knights are placed on the four corners of the board then the number of possible solutions is maximal, it is 800!
From E. Gik, Chess and Mathematics, Quantum Library (in Russian)
Mar 20, 2017
0
#7
Yes, @The_Chin... the shapes and the number of squares in the figures must be the same. Two shapes of the same area are considered the same if it is possible to cover one figure by the other by rotating and shifting the second one.
Mar 20, 2017
0
#8
@MechHand :-) We are interested with the number of solutions that can not be obtained from each other via mirror symmetry, rotation, change of colors of squares or pieces.
Mar 20, 2017
0
#9
I guess I have a try. I don't see how it can be anything other than a spiral type of shape though.
Mar 20, 2017
0
#10
Interesting solution. Your shapes have been separated into two parts. I do not think it is allowed in the statement of the problem. Let us try to find plane figures without separate parts.
Four Knights Problem
Divide the board into four regions of equal shape so that each knight belongs to one of the regions. One of the possible answers is the following:
Can you find the other solutions of this problem? Write in the comments. If the knights are placed on the four corners of the board then the number of possible solutions is maximal, it is 800!
From E. Gik, Chess and Mathematics, Quantum Library (in Russian)