The formula for the system would be very simple.



Is the system outlined above legitimate and fair?
First of all it is legitimate because rating systems are constructed in such a way that the difference between the strength of players is characterized by the absolute difference between their ratings. Roughly speaking this means that an 1400 has the same chance of beating an 1200 as an 1800 would have to beat an 1600. This means that deducting the same amount of rating points from every player rating does not alter their strength relative to each other within the pool ( the rating system is invariant to deducting a constant from every rating ).
But is this system fair?
I argue that it is fair because the phenomenon of rating inflation/deflation is unfair. If for example in correspondence chess a novice player launches a large number of games on a 'why not?' basis and then simply abandons them and loses them on time and later closes his/her account this contributes to an unfair inflation of ratings within the pool. The players in the pool do not deserve their high rating because they did not achieve them by winning actual games. Also when a very high rated player is removed from the pool all the other players rating would rise according to the formula. Is this fair? In a weird sense: yes. Since by a high rated player removed from the pool there is less competition within the pool so the remaining players rightly feel that relative to the pool they got stronger. I've seen threads in this forum that demanded that the rating points of cheaters should be somehow compensated to the other players. Well: this system would do just that. If a very high rated player is banned and thus removed from the pool the rating of other players would rise according to the formula.

Last but not least here is a very well known example to the unfair nature of rating inflation.
Consider this toplist of all time high ELO ratings provided by 2700chess.com:
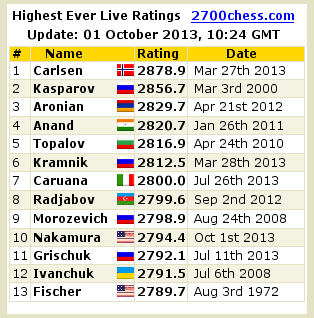
What is striking in this table is that almost all the record high ratings on this list are very recent. The only very old rating on this list is that of Fischer. The debate on the merits of Robert James Fischer is overheated and endless. But even opponents of him would agree that for him to be on an all time high list behind such players as Radjabov or Grischuk is grossly unfair.

Rating inflation may be a problem, but it is a less visible problem than subtracting from everyone's rating based on games other people have played. Can you imagine how many complaints would come from people who didn't finish any games yesterday but logged in to find they'd lost 10 points?
I'm sufficiently rusty on my calculus that I won't try to evaluate your formula for equity. Presumably you got that right.
But sometimes fairness and perceived fairness are different things. And marketing and customer retention often have more to do with perception than with hard numbers.

Rating inflation may be a problem, but it is a less visible problem than subtracting from everyone's rating based on games other people have played. Can you imagine how many complaints would come from people who didn't finish any games yesterday but logged in to find they'd lost 10 points?
I'm sufficiently rusty on my calculus that I won't try to evaluate your formula for equity. Presumably you got that right.
But sometimes fairness and perceived fairness are different things. And marketing and customer retention often have more to do with perception than with hard numbers.
10 points from day to day is way too much. We are talking of fractions of points here.
Here is real world numerical example of a 2400 cheater being removed from the pool of correspondence players here at chess.com:
| Number of players | Total number of points | Average | |
| original | 383546 | 517020008 | 1348 |
| cheater | 1 | 2400 | |
| cheater removed | 383545 | 517017608 | 1347,9972571667 |
| difference in average | -0,0027428333 |
This means that 0,0027 points should be added to every rating once the cheater is removed. Chess.com should remove almost 400 cheaters a day to account for a full point rating increase in the rating of all other players which is nonsense.
The advantage of the system that with a marginal day to day inconvenience the ratings remain comparable through long years or even decades.
As far as my formula is concerned it is very easy. If we require the average rating in the pool to remain r(p) ( the initial rating of the provisional players ) the total points in the system should be N * r(p). The actual total points in the inflated/deflated system is the sum of all ratings. In order to correct this inflation/deflation you have to remove the difference between the really existing points and the required N * r(p) points. This is the numerator of my formula. The denominator N simply says that this difference should be equally spread between players which is legitimate due to the nature of Elo/Glicko systems in which only the absolute difference of the ratings determine the relative strength.
Even if commercial sites fear that players will be angry if their rating changed a point here and there without playing a game ( but why could they not get a message stating the reason for this ? ) I still don't see why professional organizations such as Fide don't consider it.

Would be a lot of hassle for a very small problem. At the end of the day rating is way to get roughly even game. Inflatoin and deflation hit all players roughly the same way and hence is not an fairness issue.
If you want some improvement on ratings i t would need to be faster to converge. Like Bayes-Elo or similar, but inflation/deflation is not an issue, just an mior annoyance.
If rating is only to get roughly even game why would 2700chess.com publish a list of all time high Elo ratings? And why is this list hotly debated?
All time high Elo ratings should mean absolutely nothing in this interpretation ( since they compare players who don't have a chance to play against each other ).
Why is all the debate here at chess.com forums about disparity in correspondence and live ratings?
Why the demands to compansate rating points of cheaters to the other players?
The above are all due to the fact that players would really like to attribute an absolute meaning to ratings and this is by far not counter intuitive.
I'm aware fully that ratings between different eras and different pools are not directly comparable. But they should be made as comparable as possible because this is what basic intuition requires.

It is ridiculous that I have a higher percentile by almost 2 percentage points in live standard than correspondence but my rating is 160 points lower in live standard than correspondence. Yet when you hover over my nick my correspondence rating pops up as my best rating - which is my highest rating but not my best rating of which I'm proud the most. This is all due to rating inflation/deflation.
Yes this means that chess.com itself attributes an absolute meaning to ratings.
[ EDITED ]
I have just calculated that in a normalized system my standard live rating would be roughly 40 points higher and my correspondence roughly 150 points lower. So my standard live rating would end up 30 points higher than my correspondence in good agreement with my percentile. This also means that even if by theory there can be differences between pools in reality these differences are not that great ( especially if the pools are on the same internet site ).

Just maybe, some rating inflation happens because some players actually improve, without other players necessarily getting worse.
In fact, I think there are more players improving than getting worse. So, inflation happens because the pool as a whole is getting stronger, relative to (eg) a fixed strength engine rated 1600

Last but not least here is a very well known example to the unfair nature of rating inflation.
Consider this toplist of all time high ELO ratings provided by 2700chess.com:
What is striking in this table is that almost all the record high ratings on this list are very recent. The only very old rating on this list is that of Fischer. The debate on the merits of Robert James Fischer is overheated and endless. But even opponents of him would agree that for him to be on an all time high list behind such players as Radjabov or Grischuk is grossly unfair.
So if Kasparov comes out of retirement then he would be #2 in the world, correct?

Last but not least here is a very well known example to the unfair nature of rating inflation.
Consider this toplist of all time high ELO ratings provided by 2700chess.com:
What is striking in this table is that almost all the record high ratings on this list are very recent. The only very old rating on this list is that of Fischer. The debate on the merits of Robert James Fischer is overheated and endless. But even opponents of him would agree that for him to be on an all time high list behind such players as Radjabov or Grischuk is grossly unfair.
So if Kasparov comes out of retirement then he would be #2 in the world, correct?
by that logic, if fischer were to have a rating for right now, would he also be over 2700?

Kasparov's current rating is 2812. It is inactive, but he would indeed be tied for second highest with Levon Aronian. That rating would of course be soft because it hasn't been tested. And, most likely, that rating would get bashed pretty quickly. But yes, Kasparov would be #2 in the world. But he would have to prove that he deserves that rating.

The formula for the system would be very simple.
Yes, this is a good idea. Especially for the FIDE pool, which is probably going to experience some significant deflation in the coming years, because of the lowering of the FIDE floo (we already discussed this in this thread)
You may want to share your idea with the FIDE rating commission.
I propose a rating system in which the average rating of all players within the pool is always equal to the initial rating of the provisional player ( ie. the rating attributed to the player who has not played a single game yet ). The phenomenon of rating inflation/deflation would be ruled out in such a system by definition.