python simulation of candidates: pt 1

Last post I described a model for simulating the result of a chess game.  This was based on various assumptions.  One was that white gets 55% of the points in evenly matched games, which implies a 35 Elo advantage, assuming the most commonly used exponential Elo model.  The second assumption is that draw odds result in an Elo advantage proportional to the exponential of the sum of the individual player Elos.  This is based on a widely-used online calculator, which claimed draw odds are worth 0.6 pawns, and the winning chance provided by additional pawns is an exponential function of average player Elo.  So assuming draw odds reflect the chance of a draw occuring in a game without draw odds, this allowed for a calculation of draw probability between players of given Elos, higher probability for higher ranked, closely ranked players, with lower probability for lower ranked, dissimilar ranked players.

I revised the game simulation to provide results as 1 (white wins), 1/2 (draw), or 0 (black wins).  This allows me to readily sum points for a tournement.  The code returns the points won by white.  The points won by black are 1 - the points won by white.

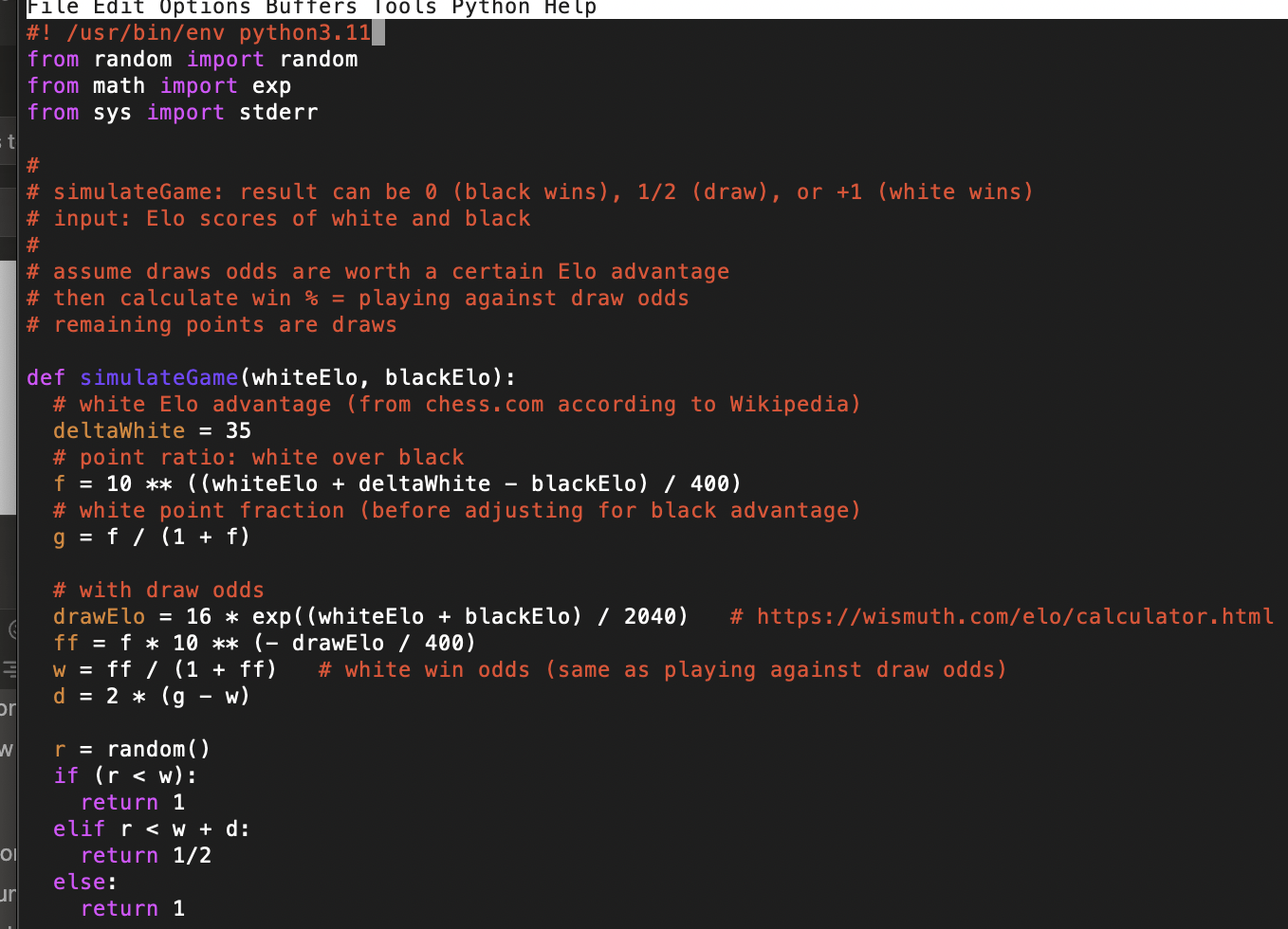
Given the game code, I can then simulate a double round-robin tournament.  In a double round-robin, players play each other player twice, and points are summed.  If there is a tie, then tie breaks are needed.  I don't calculate tie breaks yet.

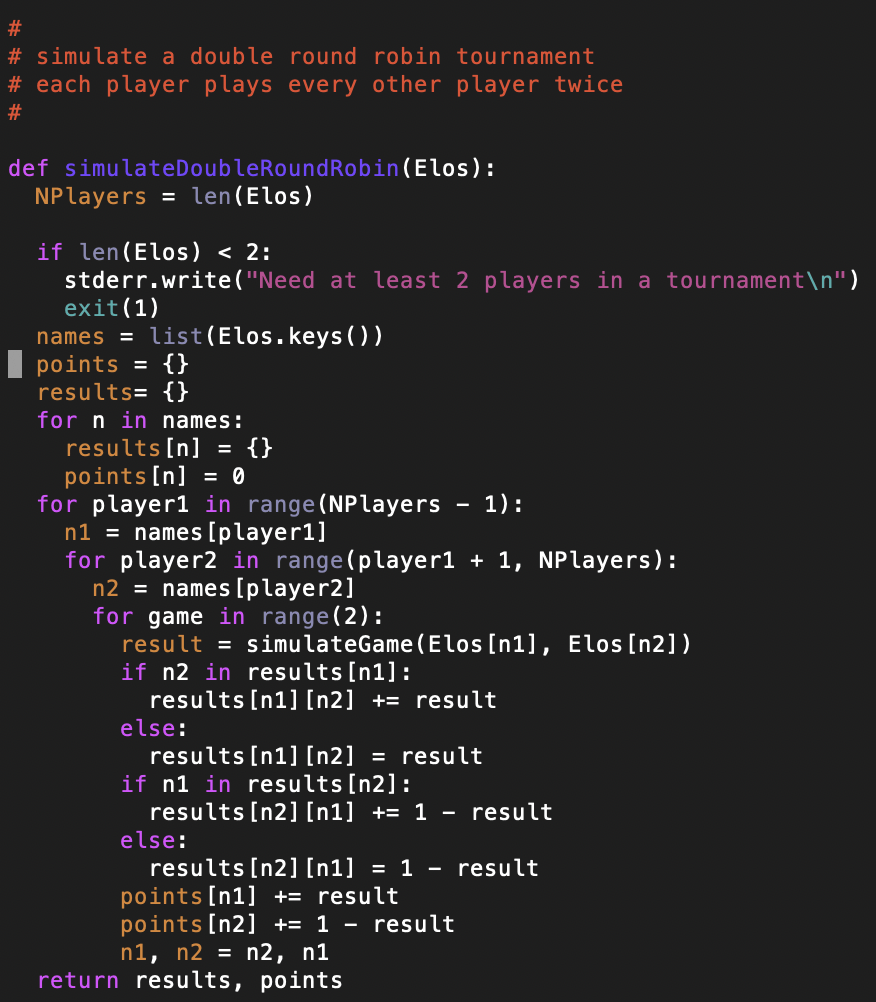
Note this plays two games per matchup, and white and black are swapped after each game.  With two games, each player plays each other player once with white, once with black.

Then I need to print out the results of the tournament.  Here's some code to do that:

Now I can apply this to a specific case.  Here I use the women's candidate tournament, where I use Elos I found on a random website.

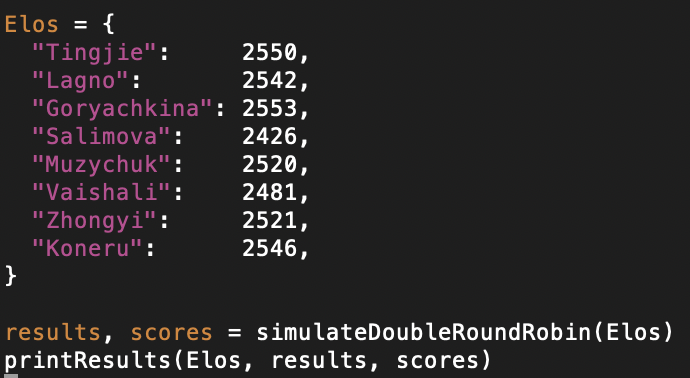
I can run this to get a typical result:

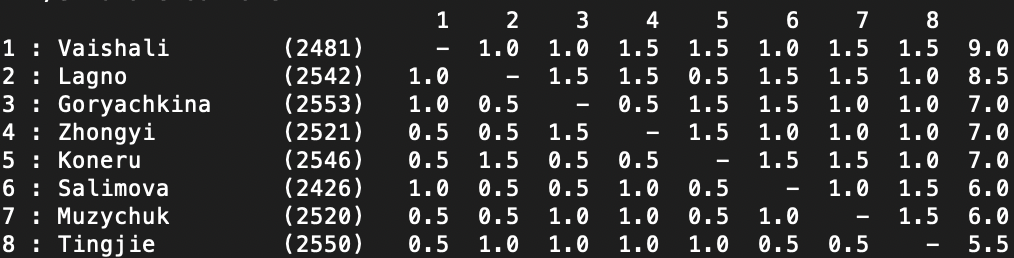
One issue is clear here: that despite the lack of tie breaks, the finishers are shown with an ordered result, which is essentially random.  I'll fix that next time.

So two additional tasks need to be done here.  One is to handle tie-breaks.  the other is to run the tournament multiple times to get statistics.  I think a million iterations of the tournament is reasonable.   For good statistics, I'd like each player to win a simulated tournament at least 1000 times, so if a player has a 1/1000 chance, to get 1000 wins, I need to run a million iterations.

I'll look at these next time.