I muddied the waters unintentionally by saying "Stockfish" when I really meant "engines" generally or "computers" (although some of this discussion about Stockfish specifically has been interesting).
The question I intended to ask is whether there are positions computers can't solve, and I think the answer is no. Engines would include programs that search the entire width of the game tree, and such engines should be able to solve any problem within their horizon which admits to a definite outcome (1-0, 0-1, 1/2). Such engines should even be able to solve chess itself, albeit on impractical timescales.



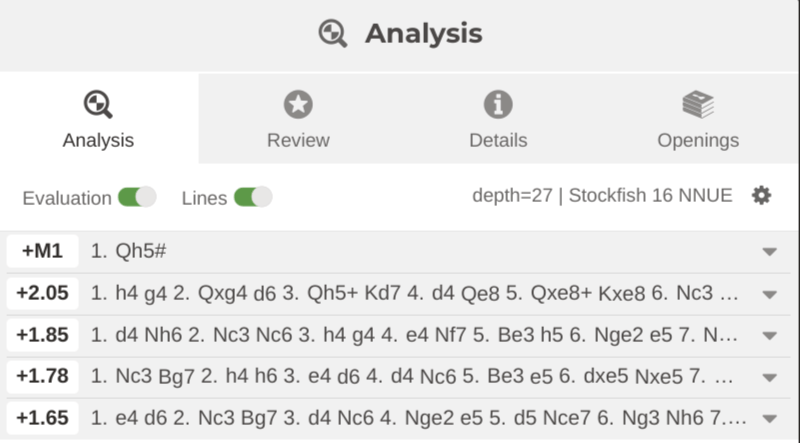
Here is another study where Stockfish is absolutely helpless (along with other engines), and has no clue as to the solution:
White to play and WIN:
We have more then one type of search that computer chess engines can use in finding a solution. Here the MCTS search gives Lc0 the answer on winning this chess position.
Line 0.0
7q/b1p5/1p1Npkb1/pPP2ppP/P1P5/3B2P1/5P1R/K3R3 w - - 0 1
Analysis by Lc0 v0.30.0:
1.hxg6 Qxh2 2.Rxe6+ Kxe6 3.g7 Qh1+ 4.Kb2 Qa8 5.Bxf5+ Kf6 6.Nc8 Kxg7 7.c6 Kf6 8.Bd7 Ke5 9.f3 Kf6 10.Kc3 Ke5 11.Kd3 Kf6 12.Ke4 Bb8 13.f4 gxf4 14.gxf4 Ba7 15.Kf3 Bb8 16.Kg4 Kg6 17.f5+ Kf6 18.Kh5 Ba7 19.Kh6 Qb8 20.Kh7 Kf7 21.Be6+ Kf6 22.Kg8 Qa8 23.Kf8 Qb8 24.Ke8 Qa8 25.Kd7 Qb8 26.Kd8 Qa8 27.Ke8 Bb8 28.Ne7 Ba7+ 29.Bc8 Kg7 30.Kd7 Kf7 31.Nd5
Depth: 30/67 00:00:22 80637kN, tb=5
White is better.
(, 02.09.2023)
Ok, so try the other ones with Lc0 MCTS (Monte Carlo Tree Search)