Calling all chess mathematicians and statisticians...need formula to indicate percentage rating rank
Sort:
I want to figure out a formula that reveals to what percentage chess belong based on their ratings. For example, if a player is 2000 then that’s an indication of belonging to the top 10% of the chess players of the world or 1500 indicates top 50% of chess players in the world, for arguments sake. Maybe we could even derive a percentile value. Granted, some of the best chess players do not have ratings. However, I think we have enough who have ratings to get some numerical percentage ratings.
I looked in the stats section of our profiles and it states my highest rating was 1714 which is an indication of a 96.6% percentile. So that means 1714 reveals the top 3.4% of all players. But how did they calculate that?
Dec 17, 2017
0
#3
What formula? you can get a percentile, but you need the distribution of the other players. The 96.6% is for the players on the website I guess...
There is no way of doing what you ask without knowing the average chess rating and the standard deviation of such ratings. If we are to assume like most things chess is distributed normally then those things are required. Otherwise we'd need to know the ratings of every single player and calculate it manually like grade boundaries. Failing that you could calculate based on a sample and work out the sample mean and sample standard deviation but then you'd need a confidence interval.
Chess ratings are more artificial than most players imagine. The numbers result from a mathematical procedure designed to rank players within a pool such that a higher-rated player is more likely to defeat a lower-rated opponent based on past performance and that's it.
Players often have the sense that a 1600 rating means something in terms in chess strength and knowledge but it really doesn't except that the statisticians sometimes tweak the model behind the curtain so the ratings are adjusted in line with player expectations. However, if the model changes or the pool of players changes, ratings can go up or down without a player's strength changing.
Here's a chart of USCF ratings for 2004 showing percentiles. Note the effect of Scholastic players.
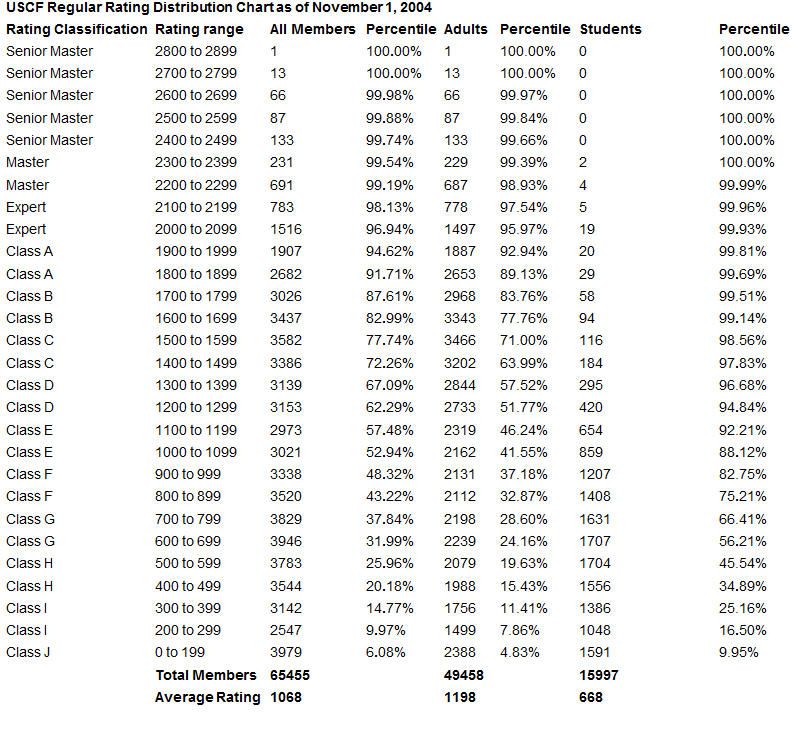
You could curve-fit a formula to spit out a percentile for a rating but it would only be guaranteed to work well with a particular player pool at a particular time with a particular rating model.
The above table of USCF Ratings in 2004 likely won't be accurate for chess.com ratings in 2017 or even USCF ratings in 2017.
Although rough guesses that USCF Masters are around 99th percentile, Experts around the 98th, Class A around the 95th, etc. are reasonable though those guesses get iffier towards the fat part of the curve.
I haven't looked at chess.com ratings much. A few years ago I had the impression that chess.com ratings lagged USCF ratings for class players. As I recall, chess.com tweaked their system about the time to shift ratings upward.
TheCalculatorKid wrote:
There is no way of doing what you ask without knowing the average chess rating and the standard deviation of such ratings. If we are to assume like most things chess is distributed normally then those things are required. Otherwise we'd need to know the ratings of every single player and calculate it manually like grade boundaries. Failing that you could calculate based on a sample and work out the sample mean and sample standard deviation but then you'd need a confidence interval.
Or that even on a normal distribution.
mgx9600 wrote:
mgx9600 wrote: Or that even on a normal distribution.
I don't follow.
TheCalculatorKid wrote:
There is no way of doing what you ask without knowing the average chess rating and the standard deviation of such ratings. If we are to assume like most things chess is distributed normally then those things are required. Otherwise we'd need to know the ratings of every single player and calculate it manually like grade boundaries. Failing that you could calculate based on a sample and work out the sample mean and sample standard deviation but then you'd need a confidence interval.
Or that even on a normal distribution.
I may have been too brief. I'm saying there's not even any indication that chess.com's rating is based on normal distribution like the original ELO rating, so without knowing the distribution function it seems premature.