
Move-Finding, The Engine Way
In a previous post I looked at how engines represent positions with bitboards. (If you haven't read that, you should!). Having a full set of 12 bitboards lets you know where all the pieces are... but that isn't the end of the story. The next step is figuring out what moves are legal in a given position. Hopefully this process will give you a deeper understanding not only of chess engines, but also of the pieces themselves.
You might not have realized it, but there are three types of chess pieces. Kings and knights move independently of the opponents' pieces (checks notwithstanding); they cannot be blocked, and if they encounter a hostile piece they simply capture it. Queens, rooks, and bishops are what we call sliders- their movement can be blocked by friendly pieces, and must halt upon capturing a hostile piece. Pawns are a bizarre combination of the first two types.
In this post I'll look first at how modern engines find king and knight moves. That process is fairly simple. Then I'll look at how they handle sliders using magic bitboards; that process is more involved.

One thing to keep in mind is that engines constantly make a trade-off between time (how long it takes the CPU to complete a task) and space (how much memory the engine would need to skip that computation). A good analogy is with opening books: It saves a lot of time to have the first few moves of the game memorized; at a certain point, however, it stops being worthwhile to memorize every line and you must begin to think.
Engines do the same thing with calculating all moves in a position. Pay attention to when they're looking something up in a table or index (space and memory) and when they're doing logical operations (time and computation). In recent years memory has become extremely inexpensive; for that reason modern engines are designed to memorize more (and calculate less) during move generation.
Now, onto the pieces! Hopefully it makes sense when I said that king and knight moves are very similar. Since their sets of attacked squares depends only on their location (and nothing else), an engine generates 64 king attack-sets and 64 knight attack-sets. This is done only once, when your engine starts; after that, the attack-sets are stored for later access.
For brevity's sake, I'll work only with knights. The attack-sets for knights on d3 and a2, respectively:

... we use the functions AND and NOT, to check which squares have a '1' in the first bitboard (possible knight moves) and a '0' in the second (locations of friendly pieces):

Success! The last bitboard above is the set of pseudolegal knight moves in the given position. Eventually we'll need to see if any of those leaves the friendly king in check, which is the difference between a legal move and a psuedolegal move. But that's easy- just make each move and test the resulting position!
Sliders are much more complicated. To handle them you need magic bitboards!
As one Stockfish developer told me (Hi Viz!), "You need to know one thing about magic bitboards: They are black magics. And they work. The end."
Another told me, "Magic bitmaps give me and many people headaches. Once you get them working they are just left alone. I have not looked at that code for many years."
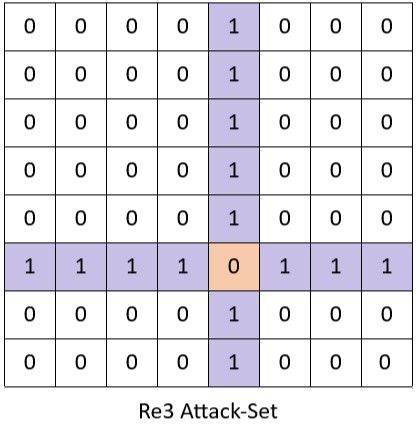
In any case, magic bitboards are used for all sliders. Let's take rooks as our example, since they are the simplest slider. We'll use the position below, with the rook on e3:
Since there are only 64 squares for the rook, we store in memory a list of all 64 possible attack-sets (as bitboards!) it might have. The attack-set we access in memory is shown below, with reference coloring; it does not yet take blockers into consideration. So far, this is working just like knights did.
The next bitboard we need is one that contains only the blockers on the e-file and the third rank. A little more processing is needed to get this bitboard, but we can just use our initial position and the Re3 attack-set. This is still a lot like what we did for knights. A nice simplification is that the four 'edge' squares can be ignored, since they never block anything. I've therefore colored them grey:
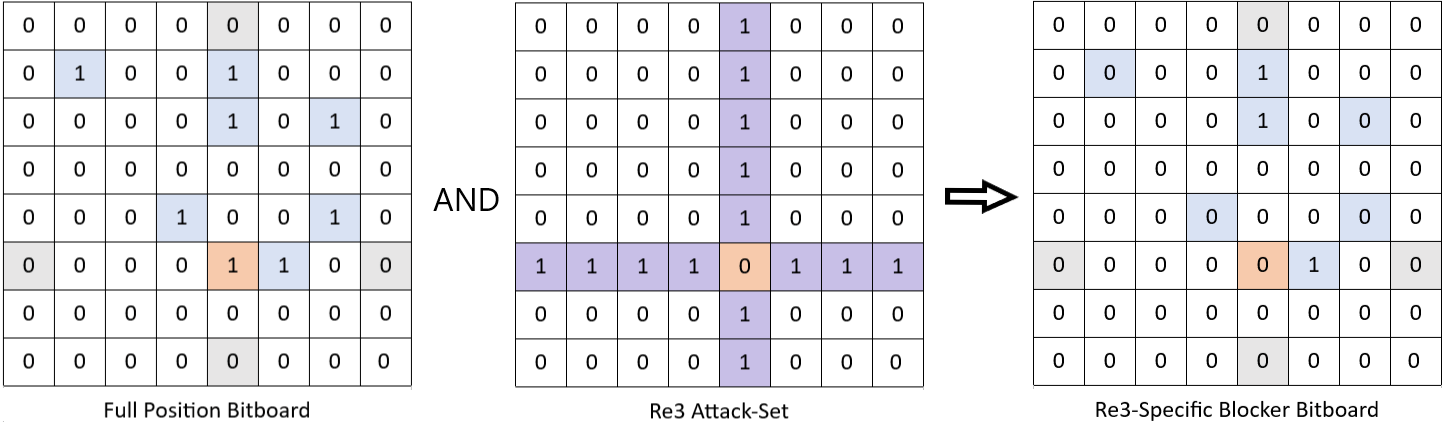
The next step is where the bitboards become 'magic.' Remember from my previous post that bitboards can be expressed as strings of bits in memory. This is the string for the Re3-blocker set that we just made:
0000000000010000000100000000000000000000001000000000000000000000
But this string also expresses a unique binary number. We can multiply that number by a magic number (a different binary string, or visualized as another bitboard) that is specific to rooks on e3, like so:

The first several bits of the index bitboard (the yellow squares) are called an index key. In this case the key needs to be 10 bits long. (Can you find the squares where a rook would need a 12-bit key?)
Each index key is associated with exactly one bitboard describing a set of rook moves. So, we take our specific key and search the index until we find a match.
That index key is guaranteed (by math or magic) to be associated with the bitboard appropriate for our position! Magic depicted below:

Finding magic numbers that give a unique index string for each combination of blockers is a difficult problem. Stockfish (for example) is designed to generate its own set at startup, but it's an open question of whether a set of smaller magic numbers can be efficiently found. Currently trial-and-error is our best method of finding new magic numbers.
Since we never differentiated between friendly and hostile blockers, we need one last step. The rook-moves bitboard from the index needs to be filtered with a friendly-blockers bitboard:

The third piece-type, pawns, are really just a combination of knight-type moves and slider-type moves. (Somehow, they also manage to be the worst piece as well.) But I'm sure you've had enough move-finding for today, so I'll leave pawns alone.
Thanks for reading! Please let me know what you think in the comments.