Coordinate Chess

I think many chess players assume that the ubiquitous Algebraic Notation in use today is a relatively new invention and supplanted the older English or Descriptive Notation that one finds in older chess books.  I believed that myself until I began to investigate the variety and origin of chess notations, which I introduced in my last blog.

However, Algebraic Notation is centuries old.  Phillip Stamma published a book in 1737, introducing Europe to Algebraic Notation.  Although the book was published first in Paris, followed by two later editions in London, the system was often referred to as German Notation, and thus not very popular in England. 

But good ideas have a habit of taking seed in the mind of intelligent people, and the advantages of “German” notation eventually overcame this cultural bias to become the lingua franca of chess today.

Just as with natural languages, there are dialects in chess languages. Most people use Short Algebraic where, except for pawns, the moving piece is indicated with a letter, followed by its destination square, e.g. 'Nf3'.  Portable Game Notation (PGN) is a dialect based on Short Algebraic and is designed to be read by chess software.  You can get a copy of PGN when you finish a game here on chess.com by clicking on the 'Moves' tab, and then clicking 'Get PGN'.  Long Algebraic includes both the source and destination squares of the moving piece, which eliminates ambiguity when more than one piece can move to the same square, e.g. 'Ng1-f3'.  Figurine Algebraic uses icons of the chess pieces, rather than alphabetic letters.  There are several other dialects of Algebraic Notation, including several that vary according to the native language of the player.

For example, the notation ‘Nf3’ would be rendered ‘Sf3’ by German speakers, the ‘S’ standing for ‘Springer’, which means ‘jumper’ in German, an appropriate name for the knight.  Wikipedia has a nice table to see the names and abbreviations for chessmen used in 50 languages.

In 1882 H. F. L. Meyer published A Complete Guide to the Game of Chess in which he introduced his ‘Universal Notation’ in an attempt to eliminate these regional dialects.  He wanted chess players in all countries to use the same letters ‘K’ through ‘P’ to designate the chessmen, and suggested names for English speakers to help them remember their meaning.

Universal Notation never caught on.

Algebraic notation is an example of a coordinate system for writing chess moves, whereby each square has a unique designation depending upon its rank and file.  But there are other coordinate systems for chess notation besides Algebraic.

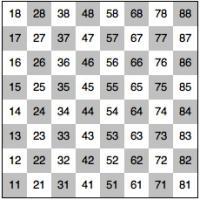
For correspondence chess, the International Correspondence Chess Federation uses a purely numeric coordinate system invented over 200 years ago by Prof. J. W. D. Wildt of Göttingen, Germany.  Each of the 64 squares is designated with 2 digits: 1 through 8 for the queenside to kingside files and 1 through 8 for the ranks beginning from the White side of the board.  This results in the following board representation:

Unlike Algebraic Notation, which combines the destination board coordinate with the piece abbreviation, e.g. ‘Nf3’, ICCF Numeric Notation or just Correspondence Notation represents each move by a 4-digit number.  The first two represent the source square of the piece or pawn and the second two its destination square.  Thus, from the White knight’s starting square, ‘Nf3’ is represented by ‘7163’.    The pawn move ‘e4’ is shown as ‘5254’.  Castling is by reference to the King move only, e.g. ‘5171’ for White’s kingside castle and ‘5131’ for his queenside castle. 

The great advantage of this notation is that it is totally unambiguous. Even Algebraic Notation has to sometimes add symbols to disambiguate moves.  If there had been a knight on d4 above, then ‘Nf3’ is ambiguous and one would have to write either ‘Ndf3’ or ‘Ngf3’ to indicate which knight is moving to f3.  No such ambiguity can arise with Correspondence Notation, nor does it suffer the regionalism of different letters to represent the pieces as was mentioned above.  For both reasons, ICCF Numeric Notation is the approved system for correspondence chess.

A similar system was developed by Louis Uedemann in 1882.  Again each square is named by two symbols, but Uedemann used alphabetic letters rather than numerals.

Uedemann's code has the interesting property that it is mirror-image symmetric from the queenside to the kingside.  Square b3 is ‘EF’ while its kingside image g3 is ‘FE’.

Now our ‘Nf3’ becomes ‘BEFI’ and ‘e4’ becomes ‘DOGO’.  Uedemann invented this system to transmit chess moves by telegraph, but there is a flaw in Uedemann’s code when used for this purpose.

Since a telegram was a manual process performed by a person operating the telegraph, it was not uncommon for the operator to accidentally transpose two adjacent letters.  Thus, the word ‘chess’ might be incorrectly transmitted as ‘cehss’.  This would normally not be a serious issue since natural languages are padded with redundancy, not to mention the fact that the recipient could usually identify the error and easily decipher it.

But when transmitting chess moves by telegram such transpositions could lead to a serious problem.  Suppose there a Queen on c3 and the sender wants to transmit the move ‘Qf6’.  In Uedemann’s system the move should be sent as ‘IFKI’.  But if the operator were to transpose the last two letters, the message could be erroneously sent as ‘IFIK’ or ‘Qc6’.  I seriously doubt that Blackburne would have risked the cost of a telegram when a careless telegraph operator could make him look like a fool and blunder away his game.

Uedemann’s system never caught on.

A chessplayer in St. Petersburg, D. A. Gringmuth recognized this flaw and devised his own system to avoid it.  Like Uedemann’s, the Gringmuth Notation is an alphabetic coordinate system, but unlike the former system, Gringmuth’s innovation was to denote every square with a consonant first, followed by a vowel.  With this change any transposition of letters would result in a meaningless chess move, avoiding the possibility of unintentional blunders.  The Gringmuth system is recognized by FIDE to this day.

Returning to Algebraic Notation, over two years ago I wrote a blog where I investigated how many distinct combinations exist of the fundamental symbols.  For example, ‘Nf3’ is one combination that is distinct from ‘e4’, and so on.  At first I had reason to believe that there might be approximately 3,000 to 4,000 distinct combinations, which I thought was surprisingly large.

I was wrong by an order of magnitude for I had calculated that nearly 30,000 distinct combinations are possible.  However, I had made some errors in this calculation and spent some time corresponding with another player, but we never quite resolved the issue.   The calculations are tedious and I have not yet had the time nor courage to resume.  In any case, whatever the true number is, it is astonishingly large. 

Chess has a way of surprising us.