Adventures with endgame tablebases
In an earlier blog I looked at the engine Stockfish from a problemist’s perspective. Another major advance in computer chess has been the development of endgame tablebases, which in some ways are even more amazing than super-strong engines. Tablebases are essentially databases of endgame positions that have been exhaustively analysed so that their outcomes (win/loss/draw) with best play by both sides are known with certainty. Moreover, in these positions the result of every possible move has been determined precisely, and thus each winning or losing move is provided with a “depth-to-mate” number, i.e. how many turns before mate is forced. What this means is that for any tablebase position, we know its complete “truth” and how perfect play would proceed.
Early tablebases could only deal with settings of specific materials, e.g. K+Q vs K+R, but as computer performances improved, we saw the creation of general tablebases that could handle any combination of pieces up to a certain total number of units. A milestone was reached in 2012 when a Russian team used a supercomputer to generate the Lomonosov tablebases, which cover all possible endgames with seven units or fewer (barring the trivial cases of six pieces vs king). Consequently, the game of chess is more-or-less solved for such miniature positions! Here are some online resources for accessing these marvels of modern technology: (1) Nalimov EGTB - 6 pieces maximum (free); (2) Lomonosov Tablebases - 7 pieces maximum (annual subscription fee required, but free for fewer pieces); (3) Android app for Lomonosov - 7 pieces maximum (free and highly recommended).
[A fourth one is the free Syzygy Tablebases, which employs another metric called “depth-to-zeroing move” and is covered in the next instalment of this blog series. Because the Syzygy site boasts the feature of linking to specific positions, though, I am including such links for the diagrams below.]
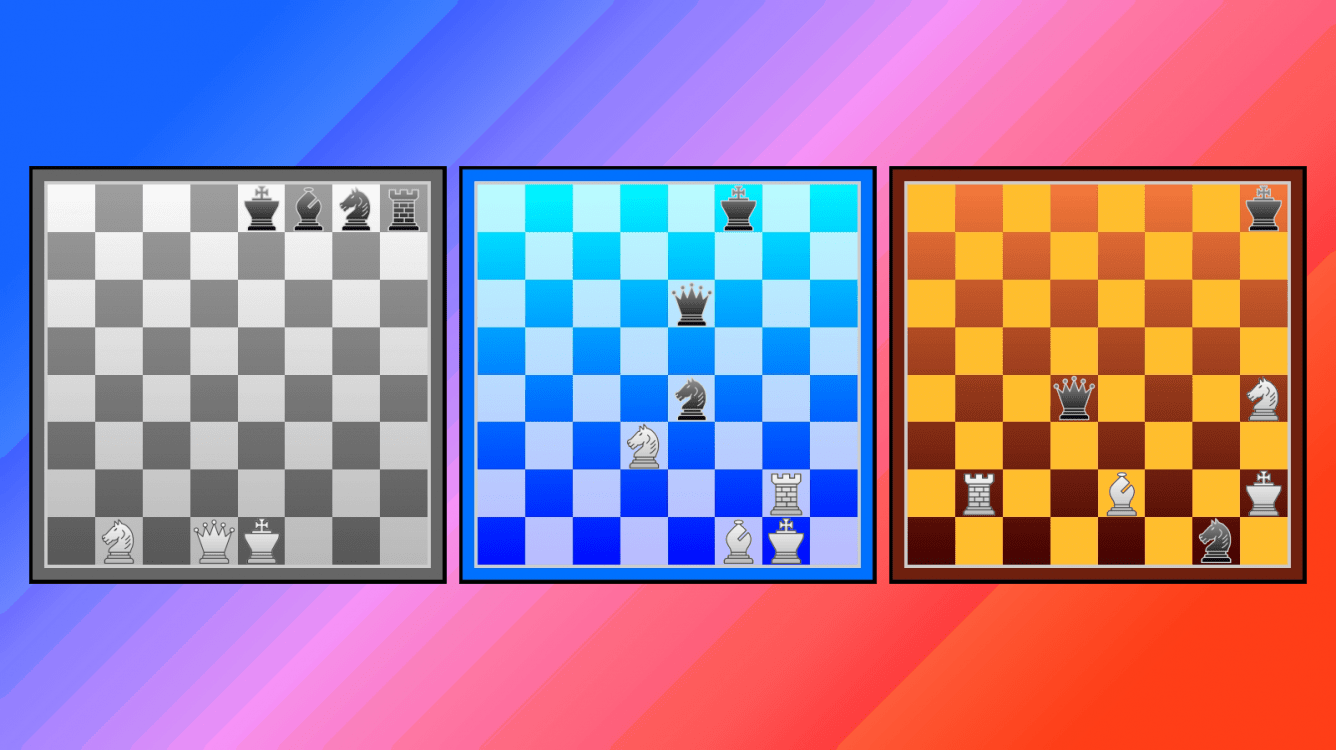
Tablebases analysis and resultant discoveries about the endgame have had a profound effect on many facets of the game; see the Wikipedia entry on the subject for details. Here I will consider how tablebases affect chess composition, and delve into three positions that illustrate what has been made feasible in problems and endgame studies. These positions employ the same material of Q+N vs R+B+N, and although I didn’t realise it at the time, this is identical to the pieces used in some length-record settings uncovered by tablebases, where to force mate requires over 500 (!) moves. My initial aim was merely to give Lomonosov some random homebase positions (all units on their array squares) to test and see if any of them would yield interesting play. The most remarkable case that I came across, with a depth-to-mate number of 90, is diagrammed below. [Syzygy TB Link]
If we treat this position as a directmate problem that requires the quickest mate to be found, a surprisingly large number of white moves in the solution are uniquely forced. In deciding on the main variation, I tried to maximise the number of such precise moves, and in the given line 77 of the 90 white moves are unique and they are marked with an ‘!’. Since “only” 13 white moves have duals, these alternatives are specified as well whenever they occur. As in most lengthy tablebase solutions, the play is not really human-comprehensible. But out of all these perfect moves, the stand-outs are three instances where the white king retreats from e2 to d1 for no apparent reason. If this were a composed problem without any duals, these recurring Kd1! (at moves 22, 32, and 41) would have been a marvellous theme!
In endgame studies, best play by both sides is assumed and since tablebases contain such perfect play information, they become a powerful resource for obtaining correct study positions. Some composers have written special programs to “mine” tablebases and generate studies that meet the criteria of soundness (dual-free variations) and interest (certain themes displayed). This method of composition is contentious for obvious reasons, but regardless, you can see some striking results of this approach in the problemist Árpád Rusz’s blog. Sometimes it’s even possible to “discover” a study by chance simply by examining the tablebase analysis of a random position. In the solution of the Mate-in-90 problem above, it’s mentioned that 41.Kf1? allows Black to draw. It turns out that the way in which Black forces a draw here is both precise and special - sufficiently so to work as a study. Here is the position in question, reflected and with the colours reversed: [Syzygy TB Link]
How does this tablebase-produced study compare with existing compositions that involve the same material? The Chess Endgame Study Database, which enables searches based on the exact material used, brings up five studies with matching pieces. An examination of these varied endgames reinforces my view that the setting above is of publishable quality. However, among these examples there is an exceptional study that shows a similar kind of idea; though not an anticipation, it’s clearly the superior work thanks to its more intensive treatment of the theme, and I quote it below.
Naturally, we can set up this position on Lomonosov and check its analysis against the author’s solution. And this brings us to another salient feature of tablebases - their ability to confirm the soundness or otherwise of every miniature study ever composed. While engines like Stockfish are strong enough to solve most studies, they do so without necessarily providing certainty to the accuracy of the intended play. Tablebases can do these verification tasks perfectly and instantaneously, within the 7-piece limit. For testing directmate problems, programs like Popeye are still preferable because of the convenience of the solution files they produce, though again tablebases have a speed advantage when solving miniatures with lengthy solutions. In the case of the Matouš study here, it is proved to be sound and completely dual-free. [Syzygy TB Link]
Three different perpetual checks are arranged with great precision and economy in this wonderful study. I was delighted to find that it was selected for the FIDE Album, the anthology of the world’s best chess compositions. And as readers may have noticed, this First Prize winner was published back in 1981, well before computers were able to assist with the creation of any chess problems or studies. That’s a victory for human ingenuity, yes?

