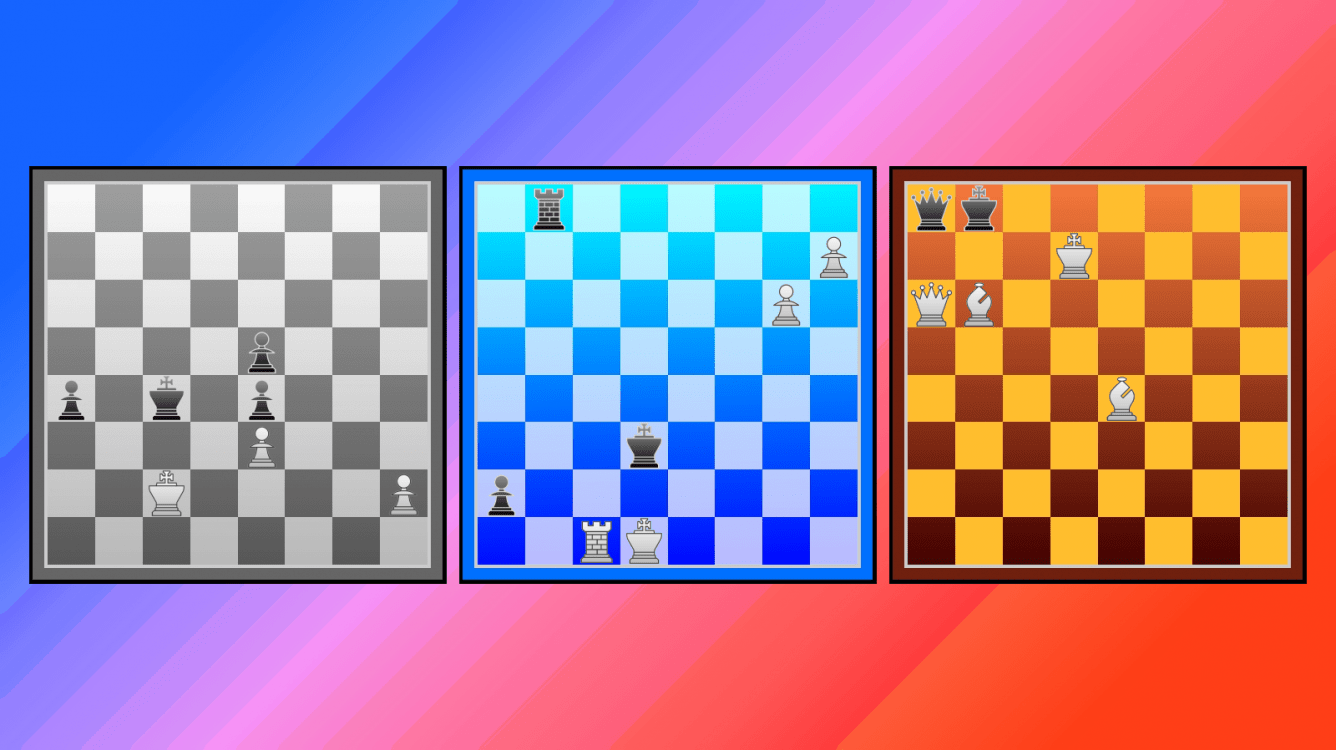
More adventures with endgame tablebases
Endgame tablebases are software that provides perfect play information with total accuracy for any position with up to seven pieces. They can determine (1) the outcome – win, loss, or draw – of every legal move in such positions based on optimal play by both sides, and (2) the precise number of moves required to force a mate for each winning or losing move. I gave a brief overview of tablebases in my previous blog and considered how they have been utilised in the field of chess composition. Here I will present three remarkable positions that came about with the aid of this tool. The first two are examples of mutual zugzwang, a paradoxical situation where neither player wants to be the side to move. The third is an offbeat endgame study that cleverly exploits not only tablebase data but also a problem convention relating to the 50-move draw rule.
In a mutual zugzwang (MZ) position, whoever has the move would prefer to pass on the turn because every possible move of each side contains a significant weakness, one that would result in a worse outcome than if the other player is to move. This curious type of situation is considered interesting in endgame theory, and tablebases have been used to systematically uncover examples. Recently the composer Árpád Rusz (mentioned in the previous post) devised a program to generate hundreds of thousands of 7-piece MZ positions, categorised according to materials such as KPPP vs KPP and KRPP vs KRP. He has kindly shared on his site these massive lists of positions, from which I select two unusual cases. Both are attractively open settings with fairly mobile pieces and passed pawns, so the double-zugzwang is especially surprising. They also illustrate the less common full-point MZ. Whereas in a typical MZ one of the players would win if it’s the other’s turn but still draw if given the move, in a full-point MZ whoever is to move would lose the game.
MZ is a popular theme in endgame compositions, but of course not all MZ positions are suitable for adapting into studies. The diagram below shows a borderline case where White’s play at some stages is too imprecise to work as a proper study, but redeeming features include a delightful key-move and a natural try that make the MZ theme hard to miss, plus a fitting finish. [Syzygy TB Link – discussed below] [White to play in MZ after 1.h3 - Syzygy TB Link]
Despite both players having a rook in the next position, neither side (if given the turn) has a waiting move that could avoid fatal self-damage. The rooks are mostly tied to their ranks as they are stopping their opponents’ pawns from promoting. White’s connected passed pawns seem very strong, but to balance that, Black has opportunities for effecting a back-rank mate. [White to play - Syzygy TB Link] [Black to play - Syzygy TB Link]
These MZ positions are extracted from the recently completed 7-piece Syzygy endgame tablebases, a free alternative to the Lomonosov tablebases. Their main difference is the metrics used to determine when a position is “won.” The more standard depth-to-mate (DTM) metric calculates the number of moves needed to achieve mate, disregarding the 50-move draw rule. Syzygy examines depth-to-zeroing (DTZ) instead: how quickly we can reach a “zeroing” move – a capture, a pawn move, or mate – that would reset the count for the 50-move rule (while maintaining the win). Now, since the 50-move draw rule doesn’t actually apply to chess compositions (see below), the DTZ metric holds no special advantage when used to analyse composed problems and studies. Indeed, for verifying directmate problems, where the quickest route to mate is stipulated, only DTM is suitable. For checking studies, which require a win or a draw to be found without imposing a move limit, the specific DTM or DTZ numbers are not that relevant, but both tablebase types are useful in revealing the win/loss/draw outcome of each possible move.
Oddly enough, our very next example contradicts what I just said about the unimportance of DTM and DTZ figures in studies! To grasp this unusual piece of work, first we have to consider how the 50-move draw rule is treated in compositions. On the World Federation for Chess Composition site, the Codex for Chess Composition states in Article 17: “Unless expressly stipulated, the 50 moves-rule does not apply to the solution of chess compositions except for retro-problems.” It makes sense for problems and studies – with their aesthetic intent and idealised play – to ignore such a rule, one based on an arbitrary number. The exception is made for retros to cover a sub-genre of problems in which it can be proved by retro-analysis (backward reasoning) that a large number of moves have taken place without a capture or a pawn move, such that the 50-move rule comes into play and it becomes part of the problem’s theme. Such retro problems involve intricate retractions and heavy positions, and seem far removed from the miniature studies we’ve been looking at, the sort where tablebase analysis is practicable. Yet by making allowance for these traditional retros, Article 17 has an unexpected consequence in certain situations, one brought to light by the composer of the following study.
By convention, the “Draw” stipulation means White is to play and force a draw, but how can that be the goal here when White has multiple mate-in-one moves? It turns out, upon further inspection, that Black couldn’t have made the last move to reach the diagram position. That’s because if the black king had just moved from a7 or b7 to b8, the piece would have been in an impossible double-check by the white pieces; and if the black queen had just come from any of the empty squares, a7, b7, c6, or d5, the piece would have been checking White while it’s Black’s turn – again an impossibility. That means, for the position to have arisen legally, White must have made the last move and it’s Black to play now. Black’s best move is 1…Qxa6 (anything else would allow White to at least draw easily). Now we have a KQ vs KBB ending, which is generally a win for the queen side. Indeed, if you were to set up this position on the Lomonosov tablebases (or the Nalimov ones), you’d find that the DTM is 69, i.e. Black has a forced mate in 69 moves against White’s best defence. So how can White achieve a draw?
Well, the study has required us to use retro-analysis to determine that it’s Black to play in the diagram. Therefore it also counts as a retro problem, and according to Article 17, the 50-move rule comes into effect! The DTM69 here is over 50 but it doesn’t actually tell us if Black could force a win under the 50-move rule, as that condition calls for a different winning strategy. This is the zeroing strategy mentioned above, where a player aims for a capture or a pawn move and thus reset the move count. We can see the exact results of this approach, viz. the DTZ numbers, by consulting the Syzygy tablebases. Here’s a link to the Syzygy site with the position already set up. Note that Syzygy also provides DTM data for positions with five pieces or fewer, but a little confusingly, they use single-move numbers (for both metrics), unlike Lomonosov and Nalimov which use the more familiar pair-move format; that’s why Syzygy indicates DTM137 for this position rather than DTM69. Now for the DTZ results, only one white move has a number higher than 100: Bc7+ with DTZ117. Thus after this bishop move, Black will need more than 50 moves to force a winning capture, but before the latter could be made, White can claim a draw under the 50-move rule as per Article 17. Therefore 2.Bc7+! is the unique drawing move. What a witty and imaginative composition! For more examples of this idea, check out its author’s Endgames to make your head hurt.

