Consecutive double-check records in problems
The theme of a chess problem often involves a recurring motif, where certain effects are repeated in a variety of ways. Since checks are one of the most basic tactical effects, it’s natural to consider multiplying them as the focus of a composition. One example of such an idea is to produce the highest number of double-checks in a directmate problem. Maximising any sort of effect takes us to the realm of task and record problems, where composers informally compete to achieve the most extreme version of a given theme. In this case, a classic work by the great Alain C. White rendered an impressive sequence of eleven double-checks, all occurring consecutively. This record held for some eighty years before it was broken twice by modern problemists, who built upon the mechanism discovered by White.
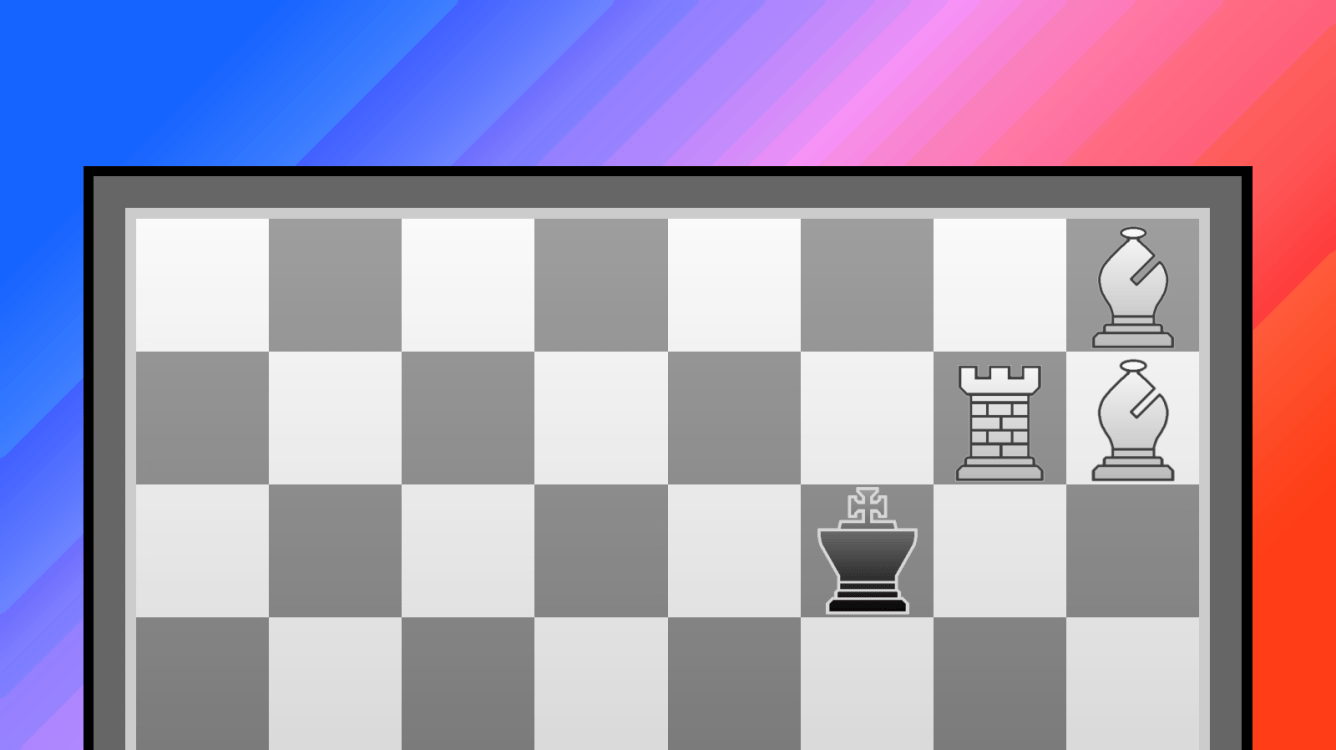
The peculiar position is fitting with the amusing solution, in which the white rook seems to chase the black king as they zigzag across the board. 1.Rf2+! Ke3 2.Rf3+ Ke4 3.Re3+ Kd4 4.Re4+ Kd5 5.Rd4+ Kc5 6.Rd5+ Kc6 7.Rc5+ Kb6 8.Rc6+ Kb7 9.Rb6+ Ka7 10.Rb7+ Ka8 (10…Ka6 11.Ra7) 11.Ra7+ Kb8 12.Ra8. Eleven double-checks are brought about as the rook repeatedly opens and closes two bishop lines, to force the king to b8 where it gets mated. The construction is excellent: White’s force consists solely of the three thematic pieces besides the king, while the whole black army serves to restrict the movement of its king. A tiny quibble is that the mating move is not a double-check; ideally a black unit should stand on b8 so that the solution ends sooner with 10…Ka8 11.Ra7 mate, to make all of White’s moves double-checks. Alas, Black is out of pieces!
The play begins nicely with an underpromotion double-check, 1.c8=N+! Kf6. Thereafter the solution largely follows the precursor problem, using the same rook-and-bishops batteries to corral the black king: 2.Rg6+ Kf5 3.Rf6+ Ke5 4.Rf5+ Ke4 5.Re5+ Kd4 6.Re4+ Kd3 7.Rd4+ Kc3 8.Rd3+ Kc2 9.Rc3+ Kb2 10.Rc2+ Kb1 11.Rb2+ Ka1 12.Rb1. There is no extraneous single-check at the end – 12…Ka2 13.Ra1 is eliminated by the blocking a2-pawn – so all of White’s moves are thematic. The increase from eleven to twelve double-checks is incremental, but a record is a record!
Our third position is clearly derived from the other two, and it holds the current record of thirteen consecutive double-checks. 1.c8=N+! Kf6 2.Rg6+ Kf5 3.Rf6+ Ke5 4.Rf5+ Ke4 5.Re5+ Kd4 6.Re4+ Kd3 7.Rd4+ Kc3 8.Rd3+ Kc2 9.Rc3+ Kb2 10.Rc2+ Kb1 11.Rb2+ Ka1 12.Rb1+ Kxa2 13.Nb4. A side-variation gives a bonus double-check: 10…Ka3 11.Bb2+ Ka4 (11…Kxa2 12.Nb4+ Kb1 13.Ra1) 12.Nc5+ Kb4 13.Ba3. Let’s see how the main line contrasts with the previous problems. Because a2 is not blocked by Black, 11…Ka1 12.Rb1+ isn’t mate, but after 12…Kxa2, 13.Ra1+? isn’t mate either, because of the d1-rook. Instead, the double-checking mate 13.Nb4 utilises the a7-rook, the same rook employed in the opening double-check (aimed at the king in another direction). This ingenious touch in construction further links the first and last move of this terrific composition.

